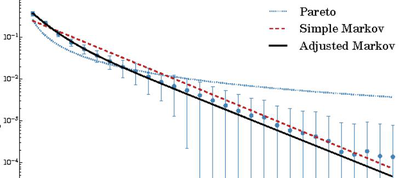
Este artículo, presenta una solución multi-objetivo del frente de Pareto para una cierta clase de cadenas de Markov controladas ergódicamente. Para resolver el problema, se transformaron los múltiples objetivos en un problema de programación no lineal equivalente que implementa el principio de Lagrange.
Luego propone adoptar el método de regularización de Tikhonov para asegurar la convergencia de las funciones de costos a un punto único en el frente de Pareto. Mostramos que las políticas de Pareto se caracterizan como políticas óptimas. Uno de los problemas fundamentales relacionados con la construcción del frente de Pareto es la existencia y caracterización de ambas, Pareto y fuertes políticas de Pareto.
Al presentar al regularizador de Tikhonov, aseguramos la existencia de políticas de Pareto fuertes. Este documento propone una solución real a este problema.
Formula el problema original teniendo en cuenta varias limitaciones: (a) se emplea el método c-variable para la introducción de restricciones lineales sobre el problema no lineal y (b) restringimos las funciones de coste, permitiendo que los puntos en el frente de Pareto tengan una pequeña distancia de unos y otros.
Las restricciones impuestas por el método de la variable c hacen que el problema sea manejable computacionalmente y la restricción impuesta por el pequeño cambio de distancia asegura la continuación del frente de Pareto.
La ecuación resultante en este sistema no lineal es un problema de optimización para el cual la condición necesaria y eficiente de un mínimo se resuelve utilizando el método del gradiente proyectado. Además, se probaron las condiciones de convergencia y se calculó la tasa de convergencia estimada de las variables correspondientes al principio de Lagrange y la regularización de Tikhonov, respectivamente.
Se proporcionaron todos los detalles necesarios para implementar el método propuesto de manera eficiente. La utilidad del método se demuestra con éxito mediante un ejemplo numérico.
Para conocer los detalles de la investigación, sólo debes entrar a la siguiente liga o buscarla mediante el DOI 10.1007/s40314-016-0360-6